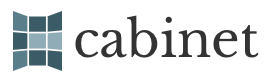Modelling retrograde motion: the theory of epicycles
External links
Commentary
The most basic astronomical problem confronting the ancient Greeks was therefore to explain retrograde motion. Two basic solutions were developed for this problem.
Nested spheres. Plato’s student, Eudoxus of Cnidus (c. 390 – c. 340 BCE) developed a means of explaining retrograde motion by using a series of nested spheres, not only for the cosmos as a whole, but for each planet. The resulting cosmological model consisted of 27 spheres: four for each of the five planets, plus three for the sun, three for the moon, and one for the fixed stars. As a rough, qualitative account of the generation of retrograde motion using Aristotelian principles; but Eudoxus’s model was not quantitatively precise. For an impression of the extraordinary ingenuity applied in fourth-century BC Athens to solving this problem, see 25:13-31:27 of the first video embedded below
Epicycles. In subsequent centuries, Apollonius of Perga (c. 240 BC – c. 190 BC) and Hipparchus (c. 190 – c. 120 BC) developed an alternative mathematical model using just two circles for each planet: the deferent and the epicycle. The deferent was a large circle with the earth as its centre, just like the orbits of the Sun and Moon. The deferent carried a second circle, the epicycle, which also rotated with uniform circular motion in the same direction as the deferent. The planet was carried by the epicycle. The combination of these two circular motions generated a pattern of retrograde motion very similar to that marked out by the five planets in the night sky.
An excellent video by the Museo Galileo (in External Links, to the right) explains how this worked. When the planet moves along the lower half of the epicycle, it travels in the opposite direction from the deferent, resulting in retrograde motion.
This arrangement also explained a second observed phenomenon: namely, that the planets appeared brightest when in retrograde motion. This made perfect sense since, within the epicyclical theory, it is while they are in retrograde motion that the planets are closest to the earth.
Limitations. Yet, for all its explanatory power, the theory of epicycles also introduced the first of a series of compromises which would eventually doom the Ptolemaic model. Planets on epicycles no longer move in simple, uniform circular motion: their motion is a more complicated combination of two different uniform circular motions. This mathematical model raises acute physical problems: it is not obvious how such motion could be generated within the nested spheres of the Aristotelian cosmos.
This criticism is implicit in Image 2, a representation of the epicyclic model of the motion of Mars from the Astronomia nova of 1609, the work in which Kepler first announced his discovering of the elliptical orbits of the plants. The same objection is even more apparent in Image 3: this representation of the combined motions of the Sun and the inferior planets, Mercury and Venus powerfully suggests the complexity and consequent implausibility of interpreting epicycles as a physical rather than a merely mathematical model. The second video below (0:43-1:53) demonstrates how these complicated patterns are generated by epicyclic theory.
Long before Kepler, this problem would eventually lead some medieval Arabic astronomers to regard the whole theory of epicycles as a purely mathematical model for calculating the movements and positions of the planets, rather than a physical explanation for those movements.
Commentary. Howard Hotson (January 2024)